Vì sao cần học toán cho lập trình đồ họa?

Không chỉ có lập trình đồ họa mà ngay cả các lập trình khác đều dựa trên nền tảng của toán học như xử lý ảnh (ngành gần với đồ họa máy tính), mạng máy tính, cơ sở dữ liệu, bảo mật thông tin, hệ thống phân tán, trình biên dịch, trí tuệ nhân tạo và máy học. Có thể bạn không thích thú lắm với toán, nhưng chúng ta không thể phủ nhận nó.

Ứng dụng của toán vào xử lý hình ảnh trong bộ phim kinh điển The Matrix,

bạn có thể code thử nếu muốn (nguồn Inigo Quilez @iquilezles)

Loạt bài về lập trình đồ họa máy tính mà mình từng đăng tải phụ thuộc rất nhiều vào các công thức, do đó mình nhận thức rõ lượng kiến thức cực lớn mà chúng ta phải trải qua. Mình sẽ cố gắng tóm tắt gọn nhất có thể, cái nào cần chứng minh sẽ chứng minh, không cần thiết mình sẽ nói nhanh qua.

Bạn sẽ ngạc nhiên khi biết rằng mấy trò chơi cực đẹp do mấy ông giỏi toán ngồi code

(nguồn @shinji_zone)

Trên thực tế, bạn cũng chẳng cần giỏi toán để viết code ảo diệu mức đó. Ở đây chúng ta chủ yếu học để biết để vận dụng vào lập trình nó, đôi khi code không ảo lắm cũng không sao.

Hệ tọa độ Cartesian trên mặt phẳng hai chiều

Từ lâu chúng ta đã được học hệ tọa độ này từ khi còn học phổ thông. Giờ chúng ta sẽ xem lại hệ tọa độ ở dạng hình hai chiều. Với x tăng về phía phải và ngược lại. Với y tăng lên trên và ngược lại

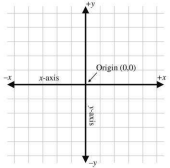Hệ tọa độ hai chiều trong toán học

(nguồn 3D Math Primer for Graphics and Game Development)

Hệ tọa độ trong nhóm hệ đồ họa OpenGL hiển thị trên màn hình

(nguồn 3D Math Primer for Graphics and Game Development)

Hệ tọa độ Cartesian trong không gian ba chiều

Ngoài 2 trục x, y ra ta có thêm trục z

Trục Z khác nhau giữa hai hệ tọa độ tay trái và tay phải 

(nguồn 3D Math Primer for Graphics and Game Development)

Trên thực tể có hai hệ tọa độ khác nhau dựa trên bàn tay trái và tay phải. Các hệ đồ họa nhóm OpenGL, Metal chỉ hỗ trợ hệ tay trái. Còn DirectX thì theo hệ tay phải, nhưng vẫn hỗ trợ hệ tay trái nếu muốn.

Với hệ tọa độ tay trái bạn giữ nguyên bàn tay như trong hình. Còn với hệ tọa độ tay phải bạn xoay bàn tay lại 180 độ thì sẽ thấy trục Z ngược hướng bàn tay trái. Lúc này trục x, y sẽ trở lại giống như hệ tọa độ hai chiều. 

Các công thức tính lượng giác cơ bản, degrees và radian

Công thức cơ bản khi tính góc trong hình học mà ta cần nhớ lại:

  • Góc 180 degree (độ) = 1 Pi Radian
  • Góc 360 độ = 2 Pi

Các công thức tính lượng giác cơ bản, ở đây ta không cần đi chuyên sâu:

cos = kề / huyền        sin = đối / huyền        tan = đối / kề

sec = huyền / kề        csc = huyền / đối        cot = kề / đối

Ta nhận ra rằng các công thức của dòng thứ hai là thương nghịch đảo của công thức dòng thứ nhất.

Công thức Pythago:

a*a + b*b = c*c

Một vài quyển sách hay về công thức toán học dành cho lập trình đồ họa

Một vài tài liệu mình tìm được khá cần thiết cho việc tham khảo công thức toán:

Comments


Comments are closed